DSSM is a Deep Neural Network (DNN) used to model semantic similarity between a pair of strings. In simple terms semantic similarity of two sentences is the similarity based on their meaning (i.e. semantics), and DSSM helps us capture that.

Semantic similarity is a metric defined over a set of documents or terms, where the idea of distance between them is based on the likeness of their meaning or semantic content as opposed to similarity which can be estimated regarding their syntactical representation (e.g. their string format)

The model can be extended to any number of pairs of strings. Here, we will take two strings as input - a query and phrase.

The figure below depicts the architecutre of the model.

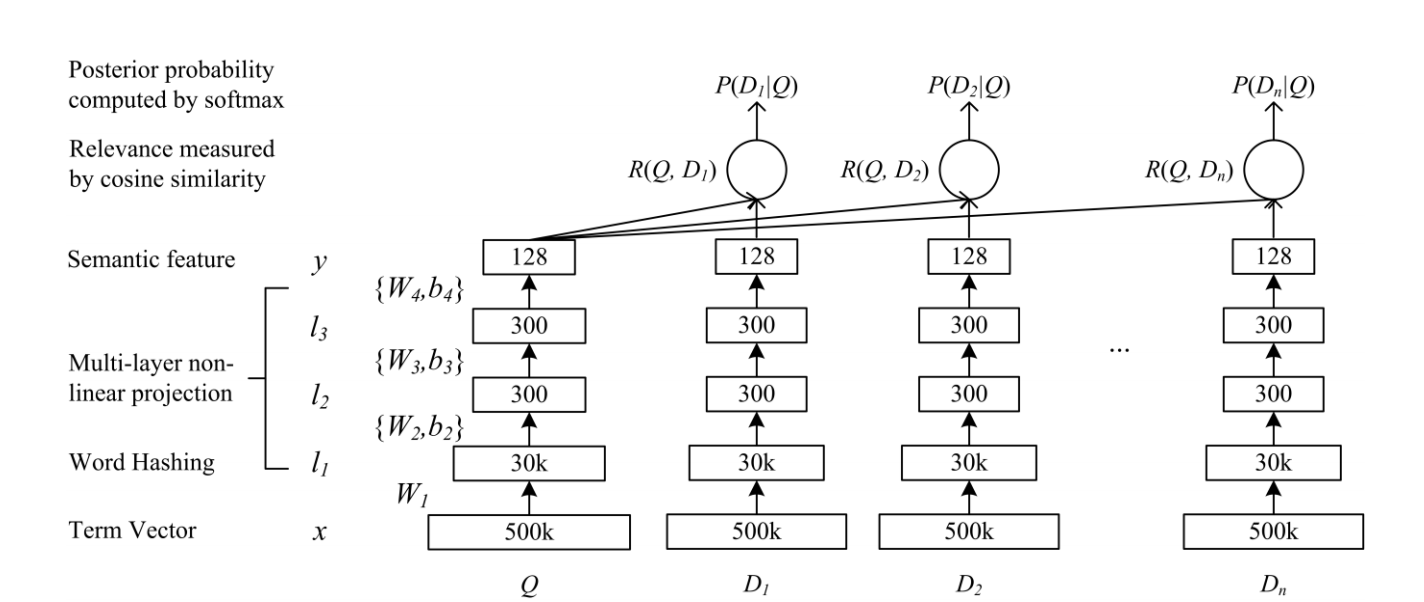
The Model

Well how do we build this model?

1. Build a bag-of-words (BOW) representation for each string (query/phrases). This is referred to as Term Vector in the figure.
2. Convert the BOW to bag-of-CharTriGrams, executed in Word Hashing layer in the figure.
3. Perform three non-linear transformation, shown as Multi-layer non-linear projection in figure.
4. The above steps are applied to each string (query/phrases) and cosine similarity is calculated for each query-phrase pair. This is the layer Relevance measured by cosine similarity in the figure.
5. Apply softmax to the outputs - Posterior probability captured by softmax in figure. The original paper uses softmax with a smoothing factor. We ignore the smoothing factor here.

A note on Word Hashing

Bag of Words representation is a poor representation of a sentence. Some of its problems are:

• It does not capture context or semantic meaning of a sentence. For instance “will this work” and “this will work” have the same BOW representation though they represent different meaning.
• It does not scale well. The size of a BOW vector is proportional to the size of vocabulary. As the vocabulary grows, the BOW becomes larger. For example, English has more than 170,000 words and new words are continuously added.

Word Hashing was introduced in the original work as a solution to the scaling problem faced by using BOW. We have more than 170,000 words in English vocabulary. Scaling becomes a problem as the current vocabulary size is large and addition of new words can make the problem worse. This can be solved if we break down each word to a bag of char-trigrams. As the number of char-trigrams are fixed and small, using a bag-of-CharTriGrams can be a good solution to this problem. To get the char-trigrams for a word, we first append ‘#’ to both ends of the word and then spilt it into tri-grams.

For the word fruit ( #fruit# ), the char-trigrams are [#fr, fru, rui, uit, it#]

Code

Now we will look into the code required for each of the steps.

1. Steps 1 and 2

   The following functions convert sentences to bag-of-CharTriGrams.

   def gen_trigrams():
     """
         Generates all trigrams for characters from `trigram_chars`
     """
     trigram_chars="0123456789abcdefghijklmnopqrstuvwxyz"
     t3=[''.join(x) for x in itertools.product(trigram_chars,repeat=3)] #len(words)>=3
     t2_start=['#'+''.join(x) for x in itertools.product(trigram_chars,repeat=2)] #len(words)==2
     t2_end=[''.join(x)+'#' for x in itertools.product(trigram_chars,repeat=2)] #len(words)==2
     t1=['#'+''.join(x)+'#' for x in itertools.product(trigram_chars)] #len(words)==1
     trigrams=t3+t2_start+t2_end+t1
     vocab_size=len(trigrams)
     trigram_map=dict(zip(trigrams,range(1,vocab_size+1))) # trigram to index mapping, indices starting from 1
     return trigram_map
   

   def sentences_to_bag_of_trigrams(sentences):
     """
         Converts a sentence to bag-of-trigrams
         `sentences`: list of strings
         `trigram_BOW`: return value, (len(sentences),len(trigram_map)) size array
     """
     trigram_map=gen_trigrams()
     trigram_BOW=np.zeros((len(sentences),len(trigram_map))) # one row for each sentence
     filter_pat=r'[\!"#&\(\)\*\+,-\./:;<=>\?\[\\\]\^_`\{\|\}~\t\n]' # characters to filter out from the input
     for j,sent in enumerate(sentences):
         sent=re.sub(fiter_pat, '', sent).lower() # filter out special characters from input
         sent=re.sub(r"(\s)\s+", r"\1", sent) # reduce multiple whitespaces to single whitespace
         words=sent.split(' ')
         indices=collections.defaultdict(int)
         for word in words:
             word='#'+word+'#'
             #print(word)
             for k in range(len(word)-2): # generate all trigrams for word `word` and update `indices`
                 trig=word[k:k+3]
                 idx=trigram_map.get(trig, 0)
                 #print(trig,idx)
                 indices[idx]=indices[idx]+1     
         for key,val in indices.items(): #covert `indices` dict to np array
             trigram_BOW[j,key]=val
     return trigram_BOW
   

2. Step 3

   We construct three Fully Connected (FC) layers of size 300,300 and 128 respectively

    def FC_layer(X,INP_NEURONS,OUT_NEURONS, X_is_sparse=False):
        """
            Create a Fully Connected layer
            `X`: input array/activations of previous layer
            `INP_NEURONS`: number of neurons in previous layer
            `OUT_NEURONS`: number of neurons in this layer
            `X_is_sparse`: bool value to indicate if input `X` is sparse or not.
                           Default value is False
   
        """
        limit=np.sqrt(6.0/(INP_NEURONS+OUT_NEURONS))
        W=tf.Variable(tf.random_uniform(
            (INP_NEURONS,OUT_NEURONS), -limit, limit), #weight init
            name="weight")
        b=tf.Variable(tf.random_uniform((OUT_NEURONS),-limit, limit), name="bias") # bias
        prod=tf.sparse_tensor_dense_matmul(X,W) if X_is_sparse else tf.matmul(X,W) #linear transformation
        return tf.nn.tanh(prod+b) # non-linear (tanh) transformation
   

3. Step 4

   Calculate the cosine similarity of each pair.

    def cosine_similarity(self,A,B):
        """
            Function to calculate cosine similarity between two (batches of) vectors
            `A` and  `B`: Inputs (shape => [batch_size,vector_size])
            `sim`: Return value, cosine similarity of A and B
        """
        Anorm=tf.nn.l2_normalize(A, dim=1) # normalize A
        Bnorm=tf.nn.l2_normalize(B, dim=1) # normalize B
        sim=tf.reduce_sum(Anorm*Bnorm, axis=1) # dot product of normalized A and normalized B
        return sim
   

4. Step 5

   Softmax and cross entropy function

    # softmax and cross-entropy
    smax=tf.nn.softmax_cross_entropy_with_logits(logits=batch_cosine_similarities, labels=Y)
   

Finally we train the model and test it on a held out dataset.